Homography vs. Perspective Transform
When to Use findHomography vs. getPerspectiveTransform in OpenCV
When working with image transformations in OpenCV, two commonly used functions for perspective mapping are cv2.getPerspectiveTransform() and cv2.findHomography(). While they may seem similar, they serve different purposes and are suited for different use cases. In this post, we’ll break down their differences, use cases, and when to choose one over the other.
Understanding Perspective Transformations
What is Homography?
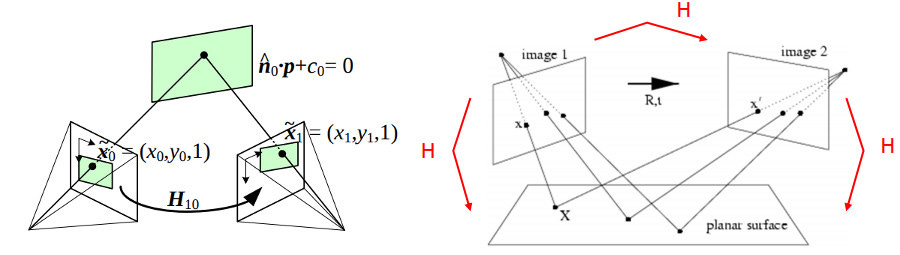
Homography is a transformation that relates two planes in a projective space. It can map one view of a planar surface to another by considering translation, rotation, scaling, shearing, and perspective distortions.
Mathematically, a homography is represented as a 3×3 transformation matrix H that maps points (x, y) in one image to (x', y') in another:
[x′y′w′]=H×[xy1]\begin{bmatrix} x’ \ y’ \ w’ \end{bmatrix} = H \times \begin{bmatrix} x \ y \ 1 \end{bmatrix}
Where:
(x, y)are the original coordinates(x', y')are the transformed coordinatesw'is a scale factor (we normalize by dividingx'andy'byw')
cv2.getPerspectiveTransform(): Simple Perspective Transform
What It Does
cv2.getPerspectiveTransform() computes a transformation matrix when you exactly know four corresponding points in both images. It assumes a pure projective transformation without considering outliers or errors in point selection.
Usage Example: Correcting Perspective in a Document Image
import cv2
import numpy as np
# Define 4 source points from the original image
pts_src = np.float32([[10, 10], [200, 10], [10, 200], [200, 200]])
# Define 4 destination points for transformation
pts_dst = np.float32([[50, 50], [250, 50], [50, 300], [250, 280]])
# Compute perspective transform matrix
M = cv2.getPerspectiveTransform(pts_src, pts_dst)
# Load image and apply the transformation
img = cv2.imread("input.jpg")
warped_img = cv2.warpPerspective(img, M, (img.shape[1], img.shape[0]))
cv2.imshow("Warped Image", warped_img)
cv2.waitKey(0)
cv2.destroyAllWindows()
When to Use It
✅ You exactly know four corresponding points between the source and destination images. ✅ You need a strict projective transformation without considering outliers. ✅ Use cases: Document scanning, billboard perspective correction.
cv2.findHomography(): Robust Homography Estimation
What It Does
cv2.findHomography() is more flexible than getPerspectiveTransform(), as it can handle more than 4 corresponding points and finds the best transformation while handling outliers using methods like RANSAC.
Usage Example: Image Stitching
import cv2
import numpy as np
# Define multiple corresponding points between two images
pts_src = np.float32([[100, 200], [300, 200], [100, 400], [300, 400], [50, 100]])
pts_dst = np.float32([[120, 210], [320, 210], [110, 410], [310, 390], [60, 120]])
# Compute homography matrix using RANSAC (robust to outliers)
H, mask = cv2.findHomography(pts_src, pts_dst, method=cv2.RANSAC)
# Apply transformation
img = cv2.imread("input.jpg")
warped_img = cv2.warpPerspective(img, H, (img.shape[1], img.shape[0]))
cv2.imshow("Warped Image", warped_img)
cv2.waitKey(0)
cv2.destroyAllWindows()
When to Use It
✅ You have more than four corresponding points. ✅ Your point correspondences may have outliers, and you need robust estimation. ✅ Use cases: Image stitching (panoramas), augmented reality (AR), tracking planar objects in different viewpoints.
When to Use Which?
✅ Use cv2.getPerspectiveTransform() if:
You have exactly four known point correspondences.
You need a strict perspective transformation.
Example: Correcting a skewed document scan.
✅ Use cv2.findHomography() if:
You have more than four matching points.
Your dataset contains outliers and requires robust estimation.
Example: Stitching images together for a panorama.
Conclusion
cv2.getPerspectiveTransform()is limited to four points and best for controlled perspective corrections.cv2.findHomography()is robust and flexible, making it ideal for real-world transformations where point correspondences might have errors.
Understanding the difference between these two functions will help you choose the right approach for your computer vision applications. 🚀
Let me know in the comments if you have any questions or if you want a deep dive into practical applications! 👇